Nothing lasts forever – only item administration: An Item Response Theory algorithm to shorten tests
\(^1\) University of Trento, \(^2\) Psicostat, \(^3\) University of Padova
Short Test Forms
Why?
Many items \(\rightarrow\) good measurement precision, great reliability and so on
Not always!
People might get tired
The aim:
\[Q \subset B\]
Item Response Theory models for the win
Being focused on the item information and on the ability of each item to measure different levels of the latent trait, IRT models provide an ideal framework for developing STF (and not torturing people)
Automated test assembly and maxmin algorithms
The 4-Parameter Logistic Model (4-PL)
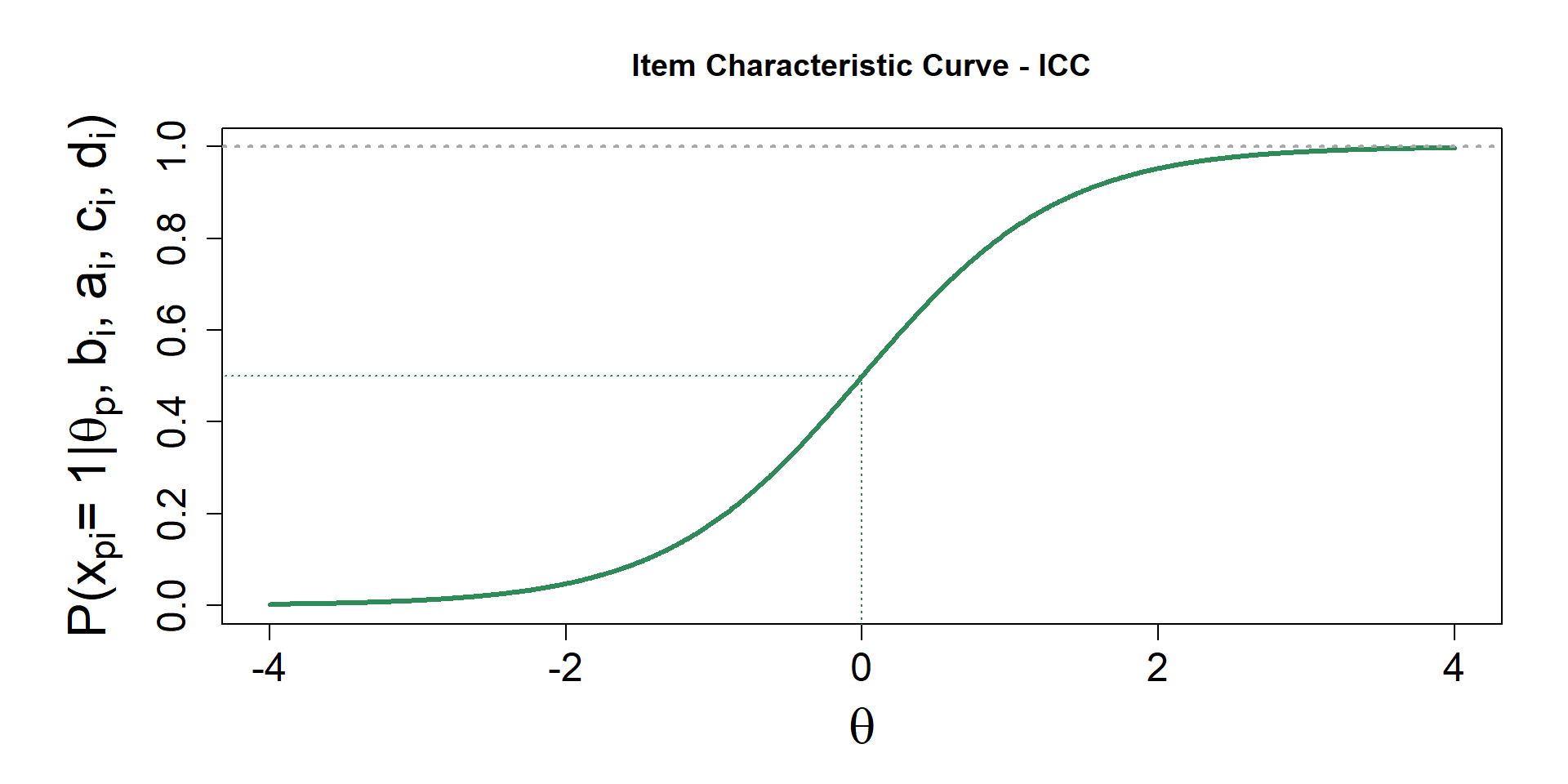
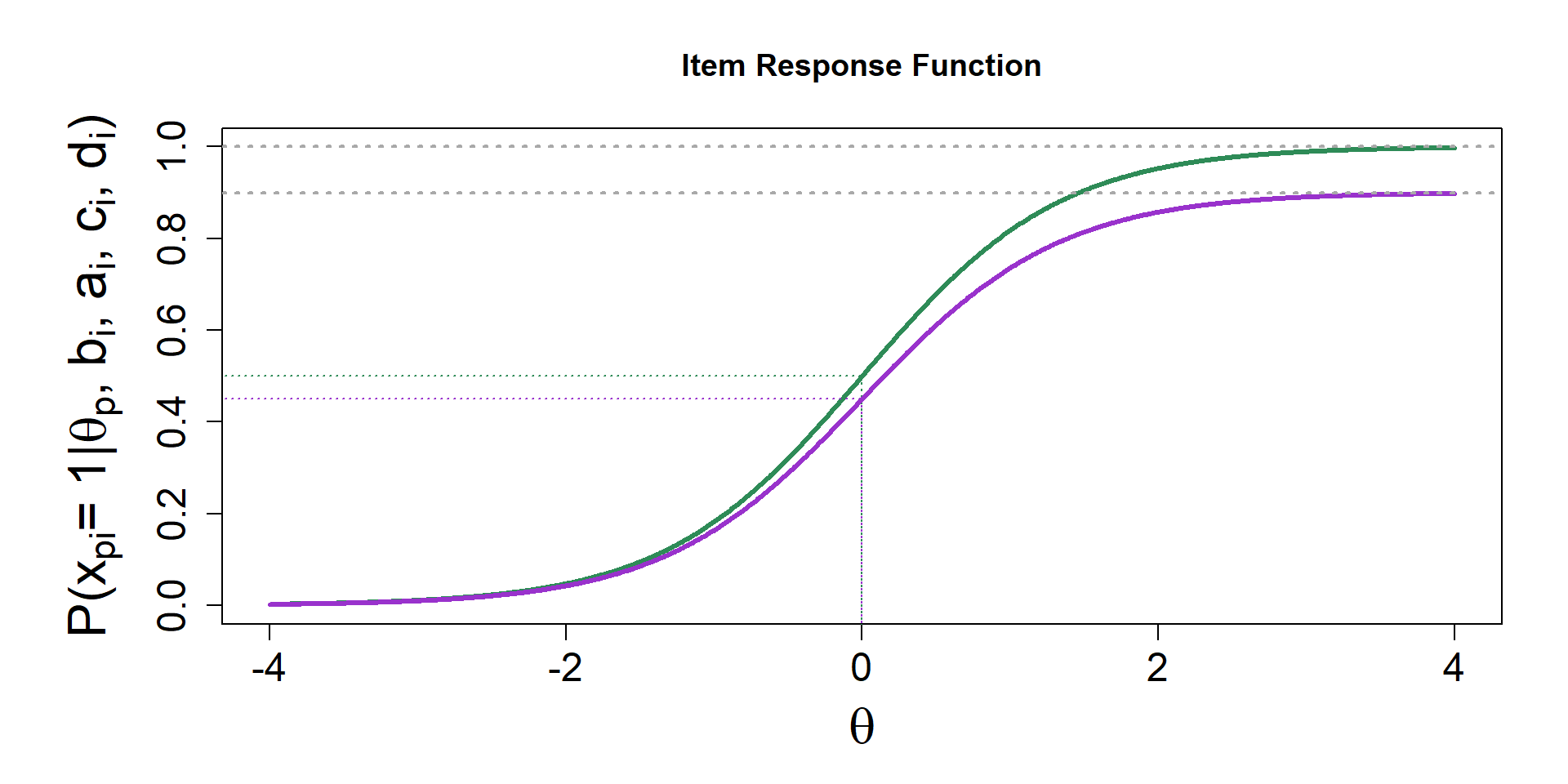
4-PL - Item Response Function
\[P(x_{pi}= 1| \theta_p, b_i, a_i, c_i, d_i) = c_i + (d_i -c_i) \dfrac{\exp[a_i(\theta_p - b_i)]}{1 + \exp[a_i(\theta_p - b_i)]}\]
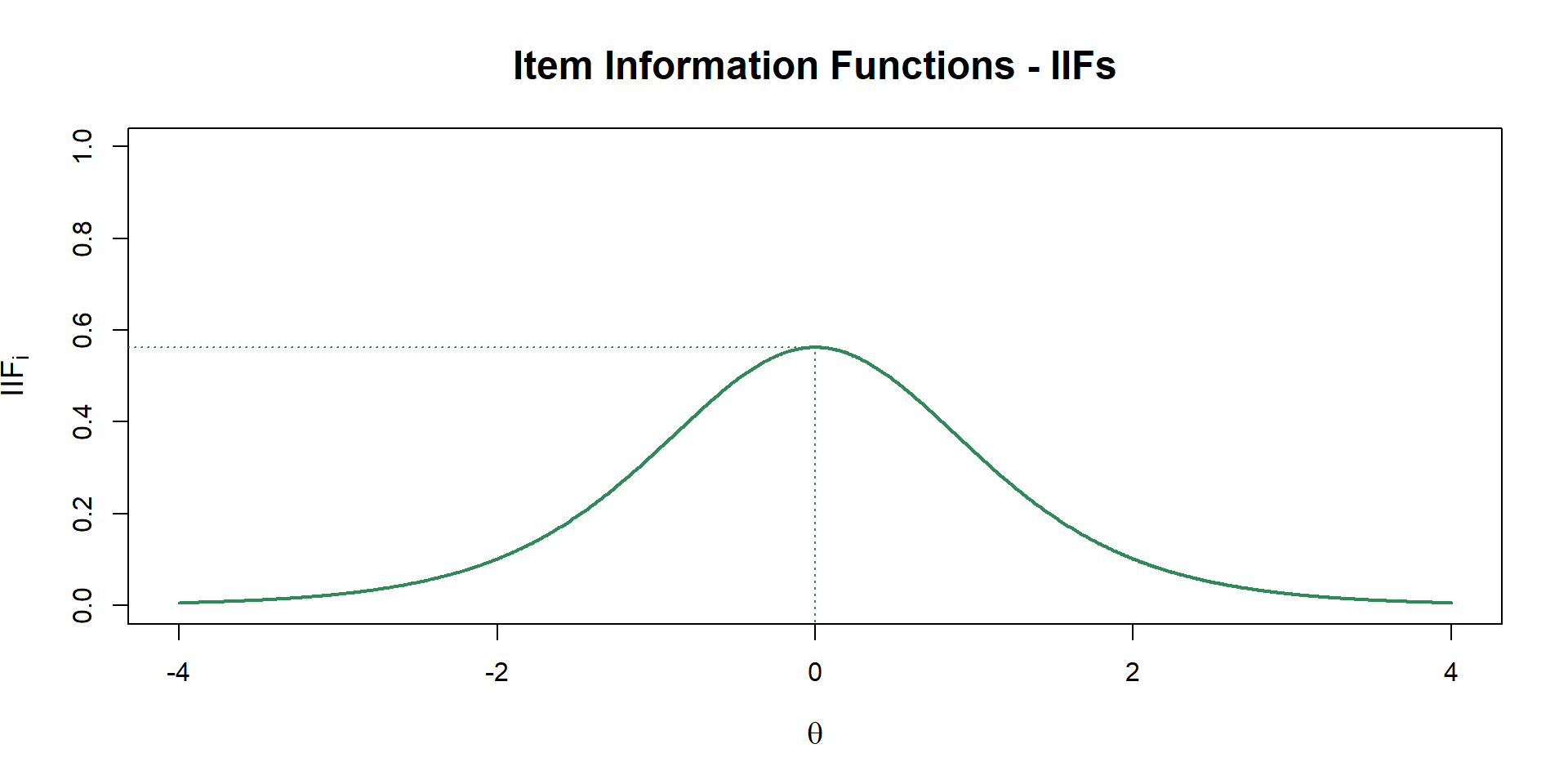
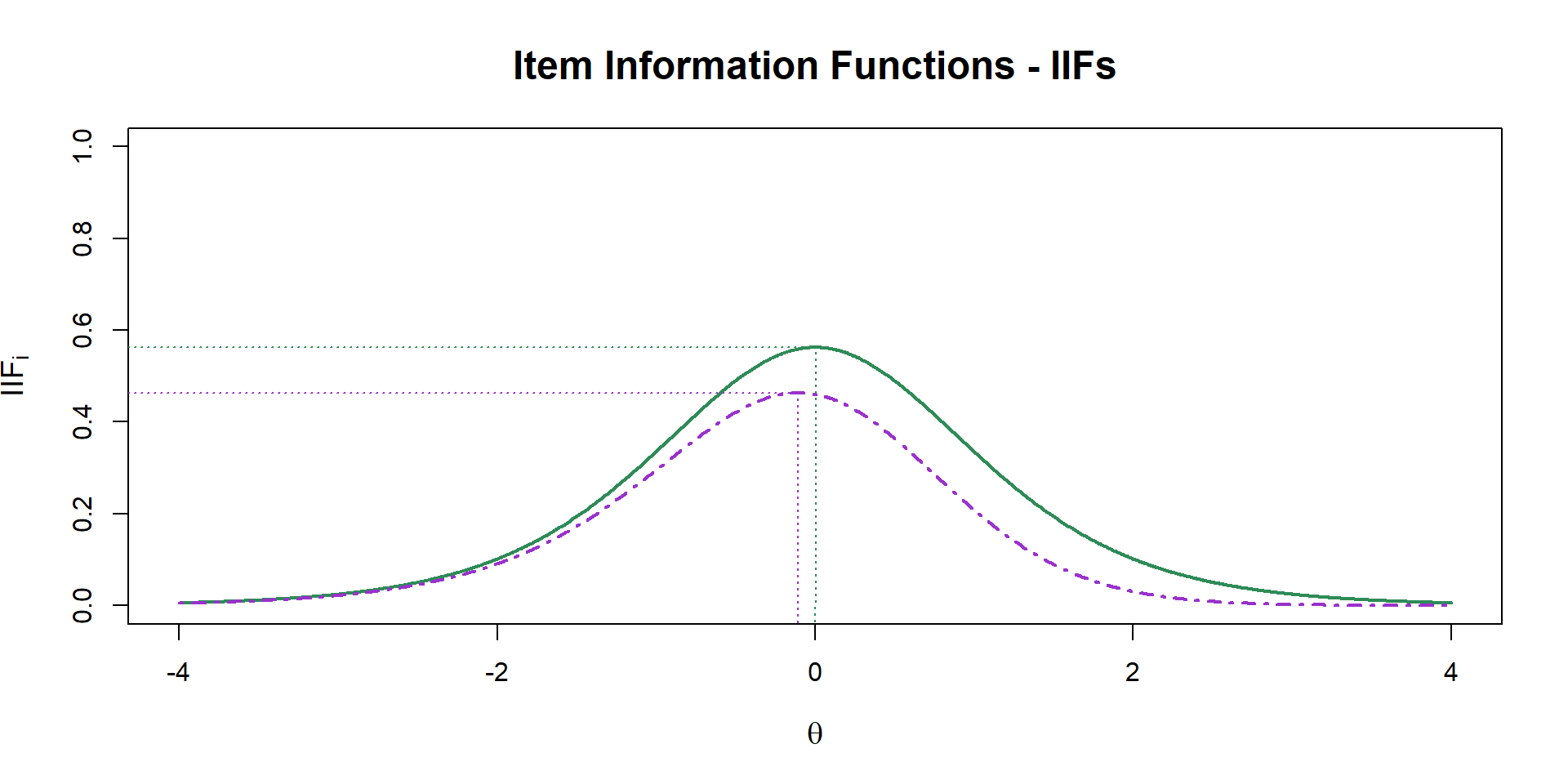
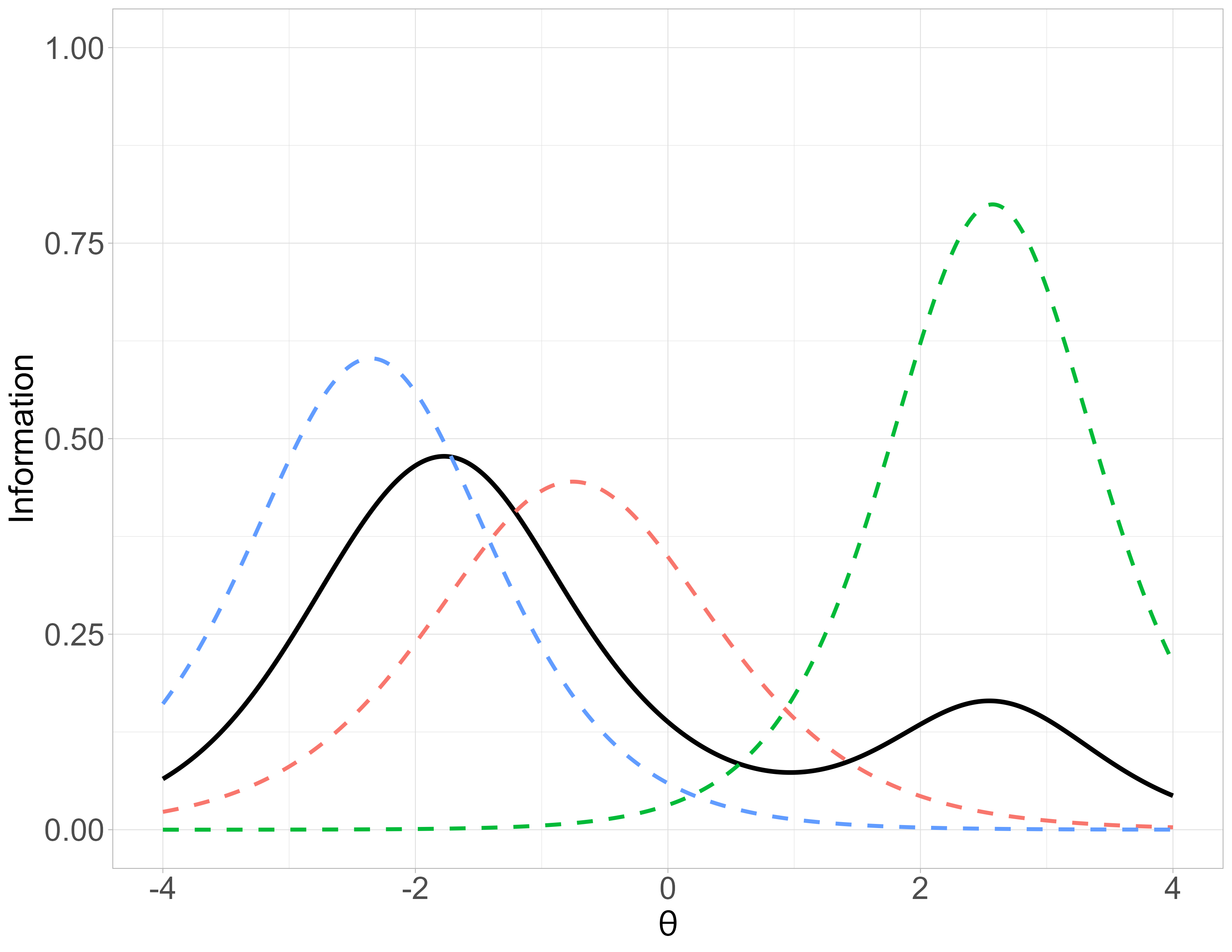
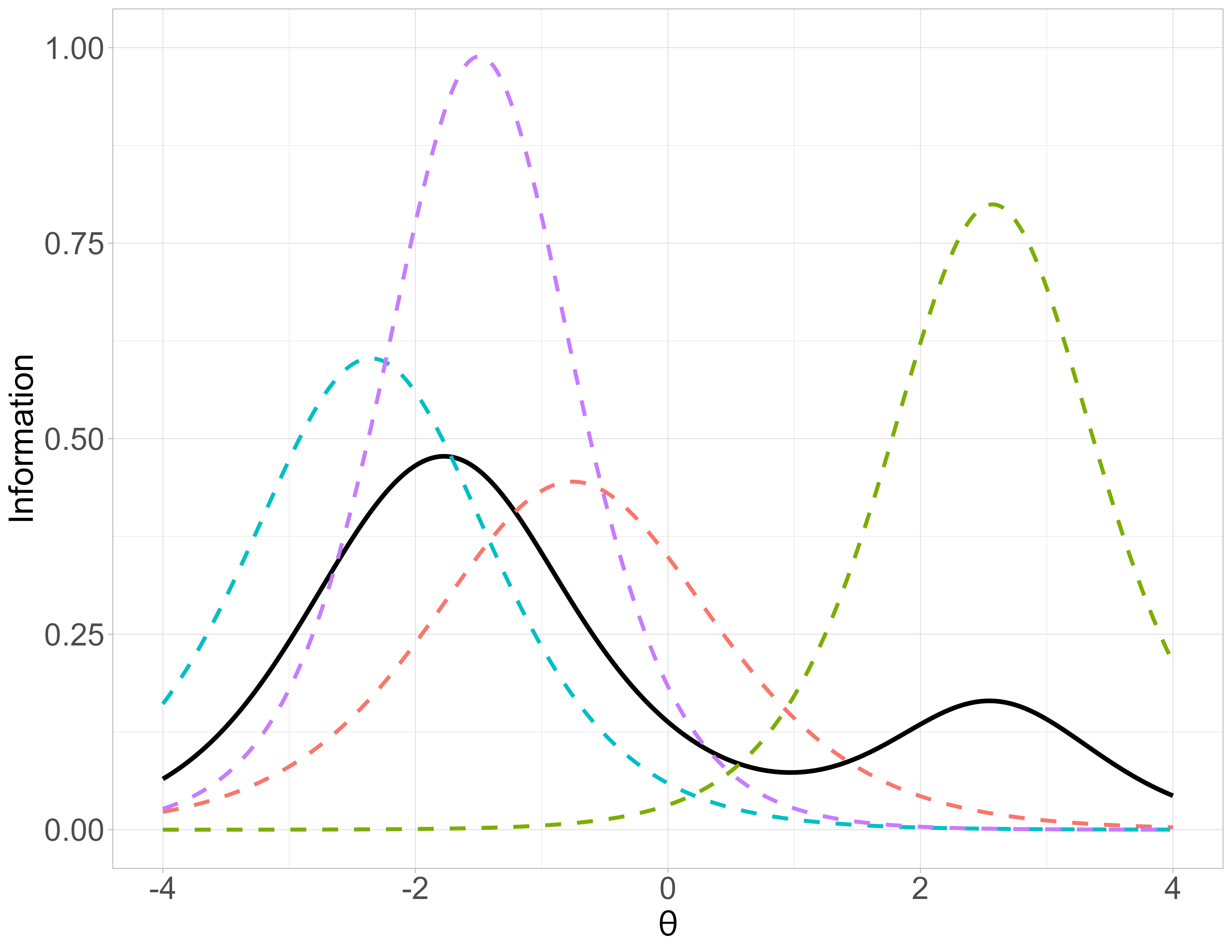
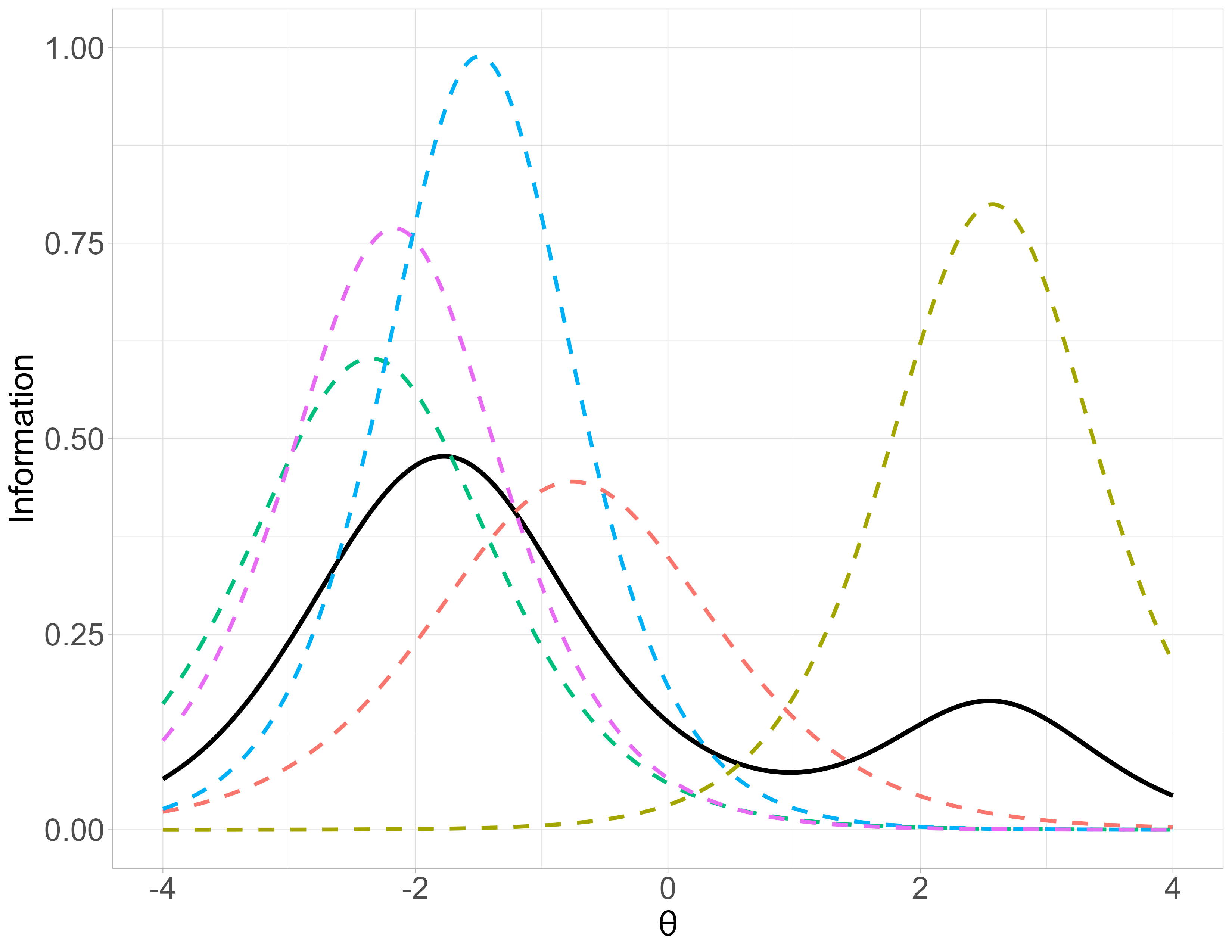
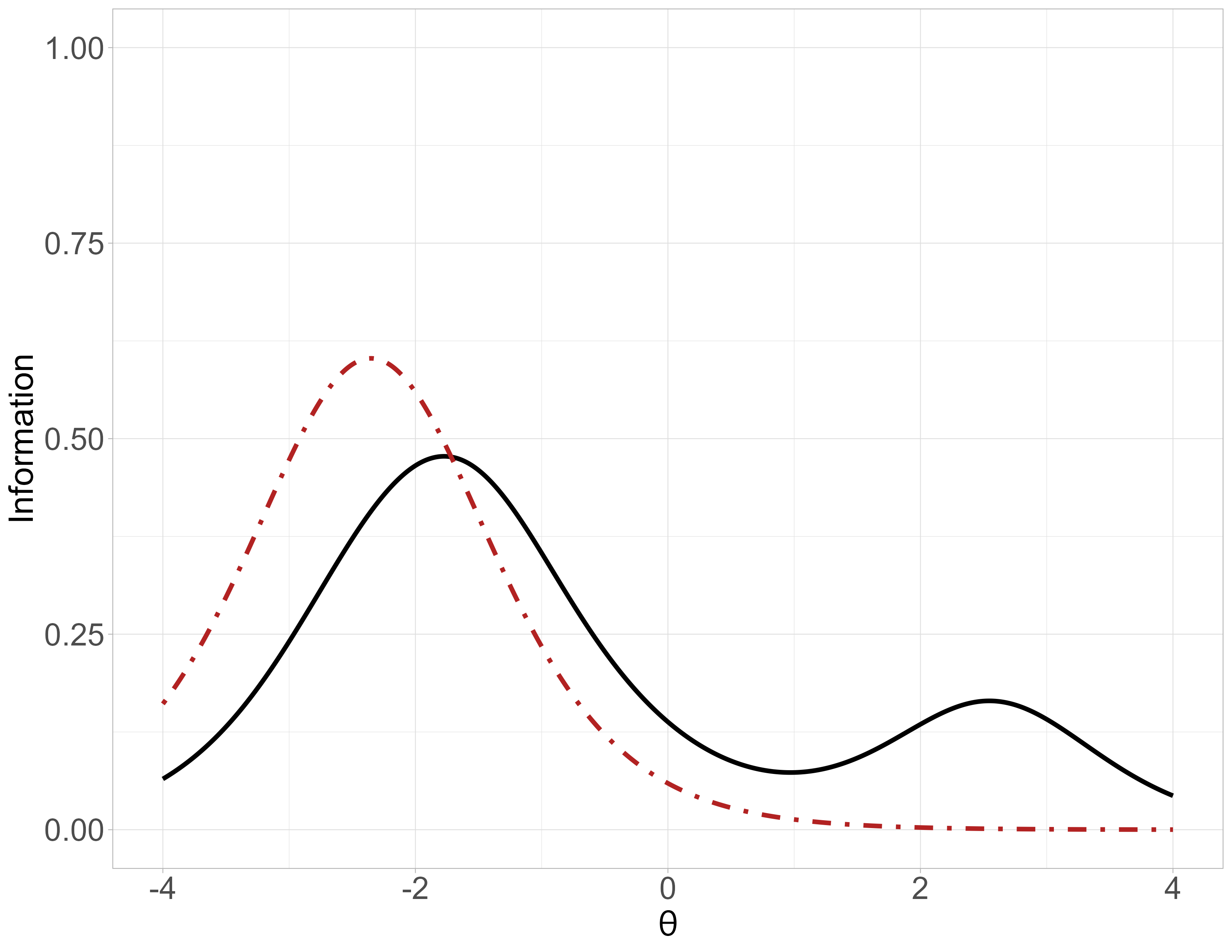
4-PL - Item Information Function
\[ \text{IIF}_{i}(\theta) = \dfrac{a_i^2[P(\theta)-c_i]^2[d_i - P(\theta)]^2}{(d_{i}-c_i)^2 P(\theta)Q(\theta)}\]
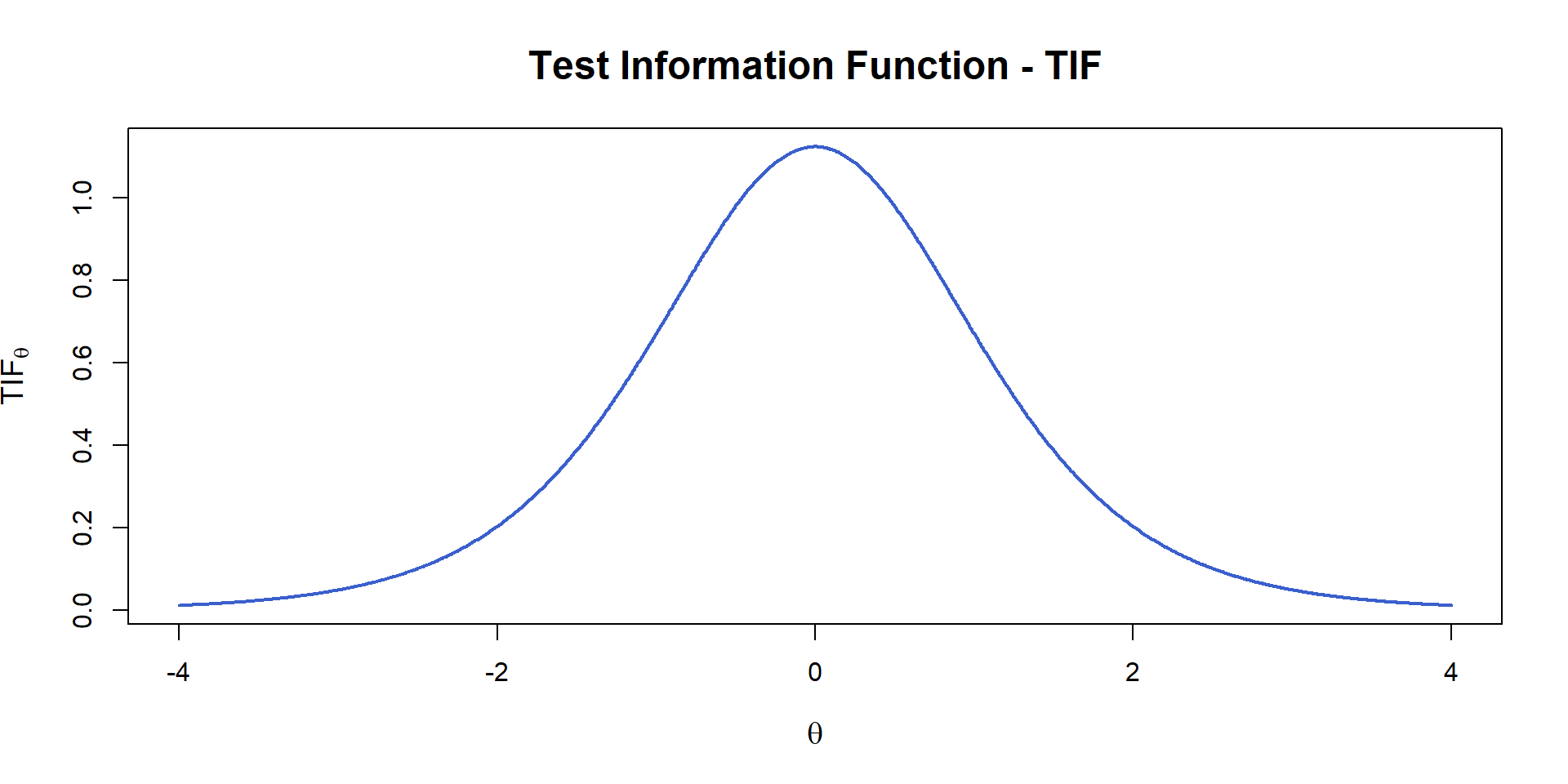
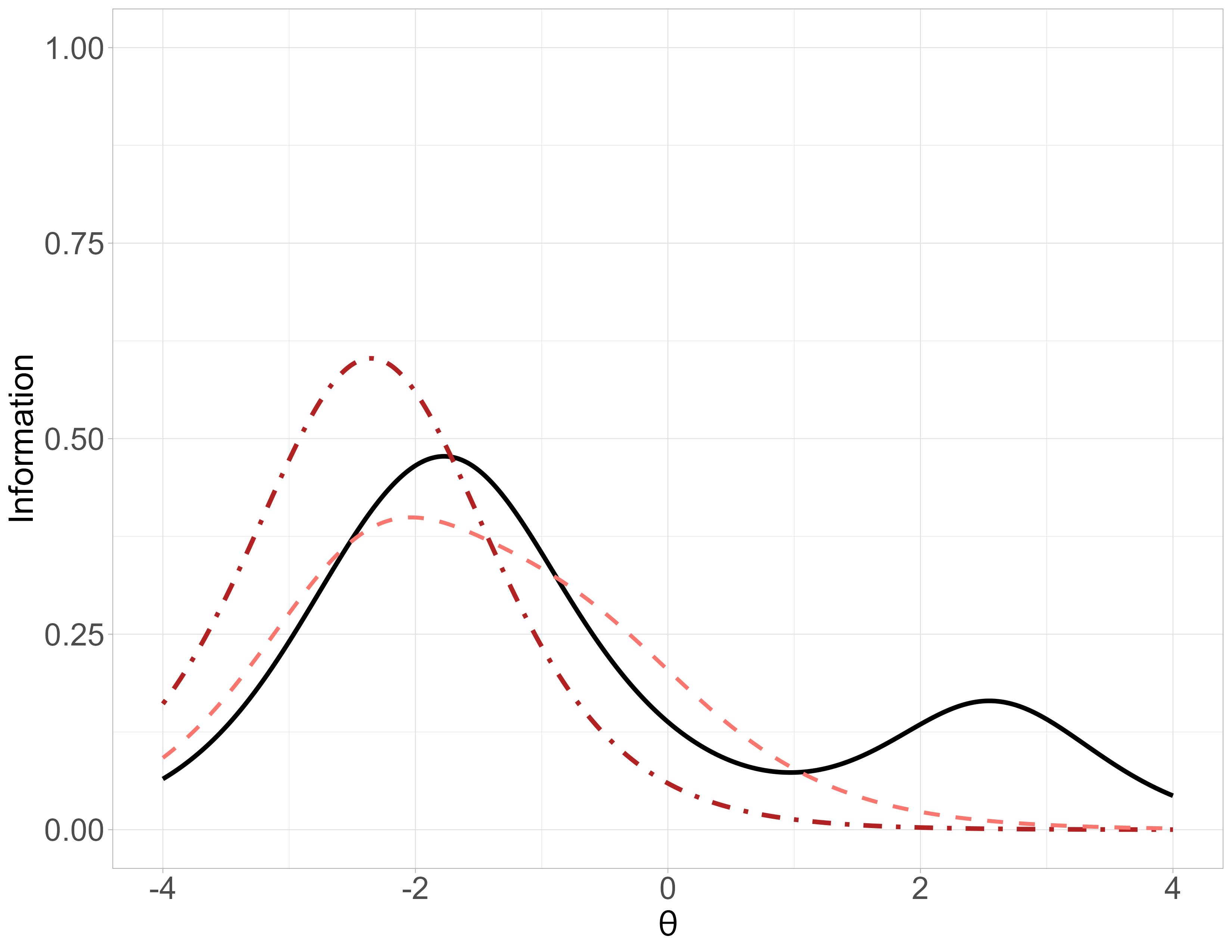
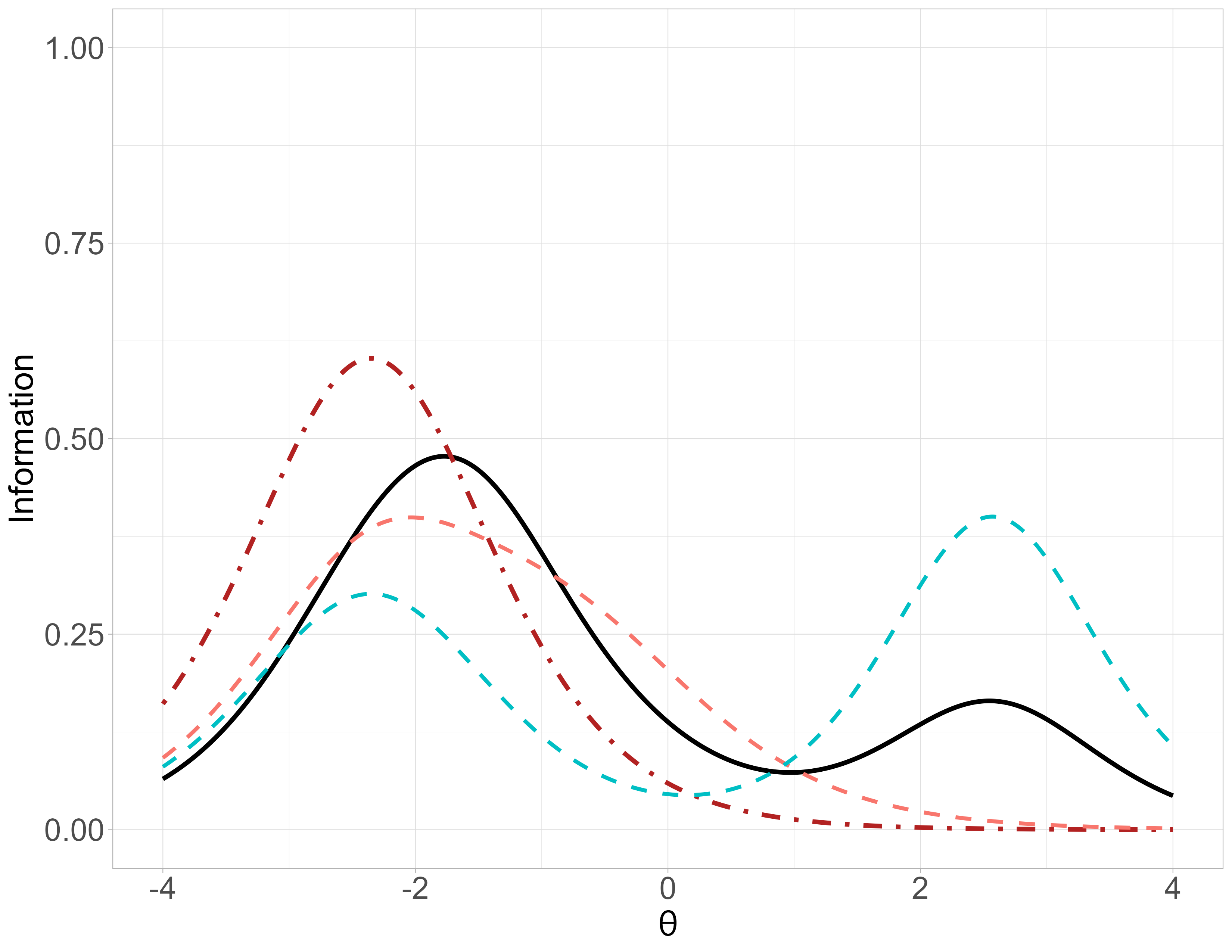
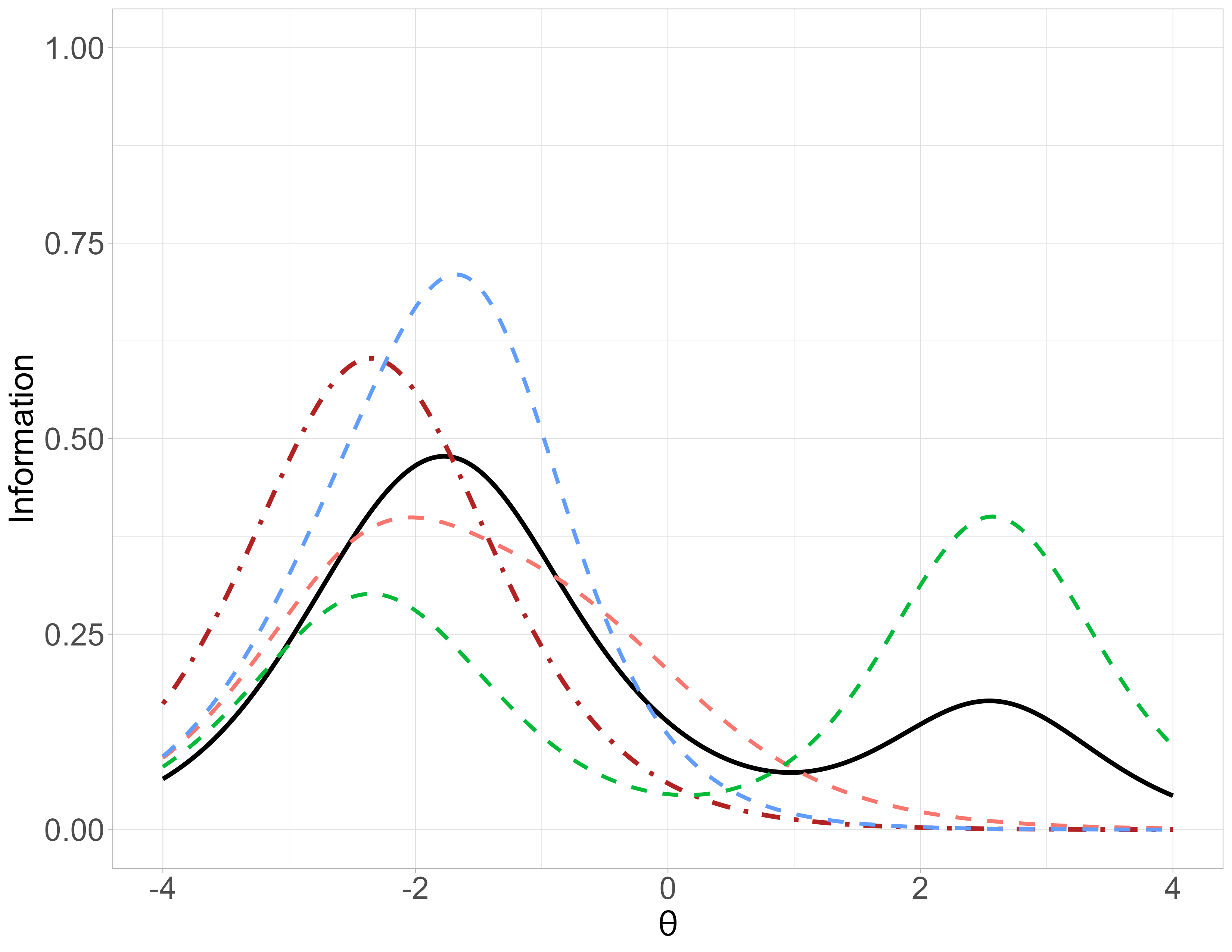
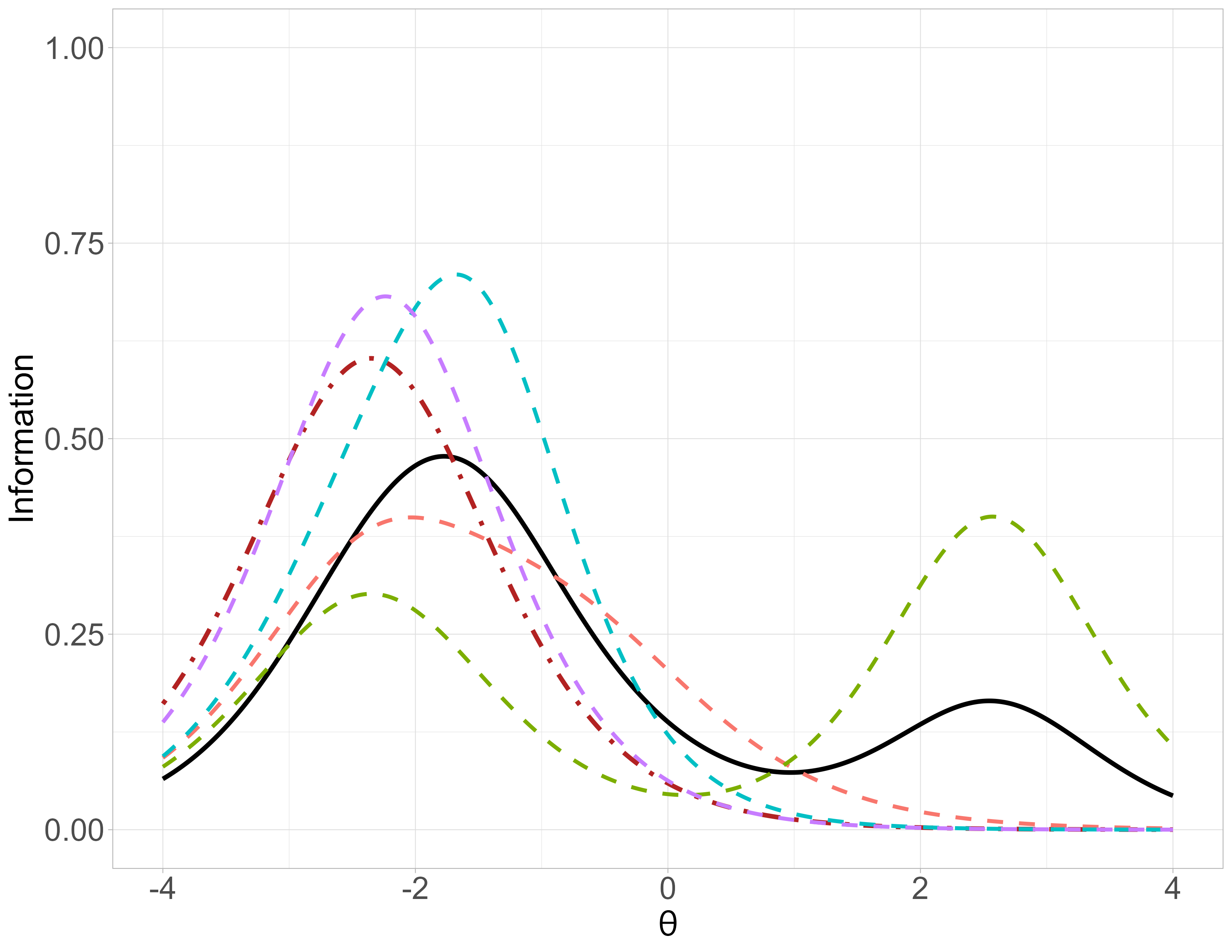
4-PL - Test Information Function
\[TIF = \sum_{i = 1}^{||B||} IIF_i\] (\(B\): Set of items in a test (\(||X||\) cardinality of set \(X\)))
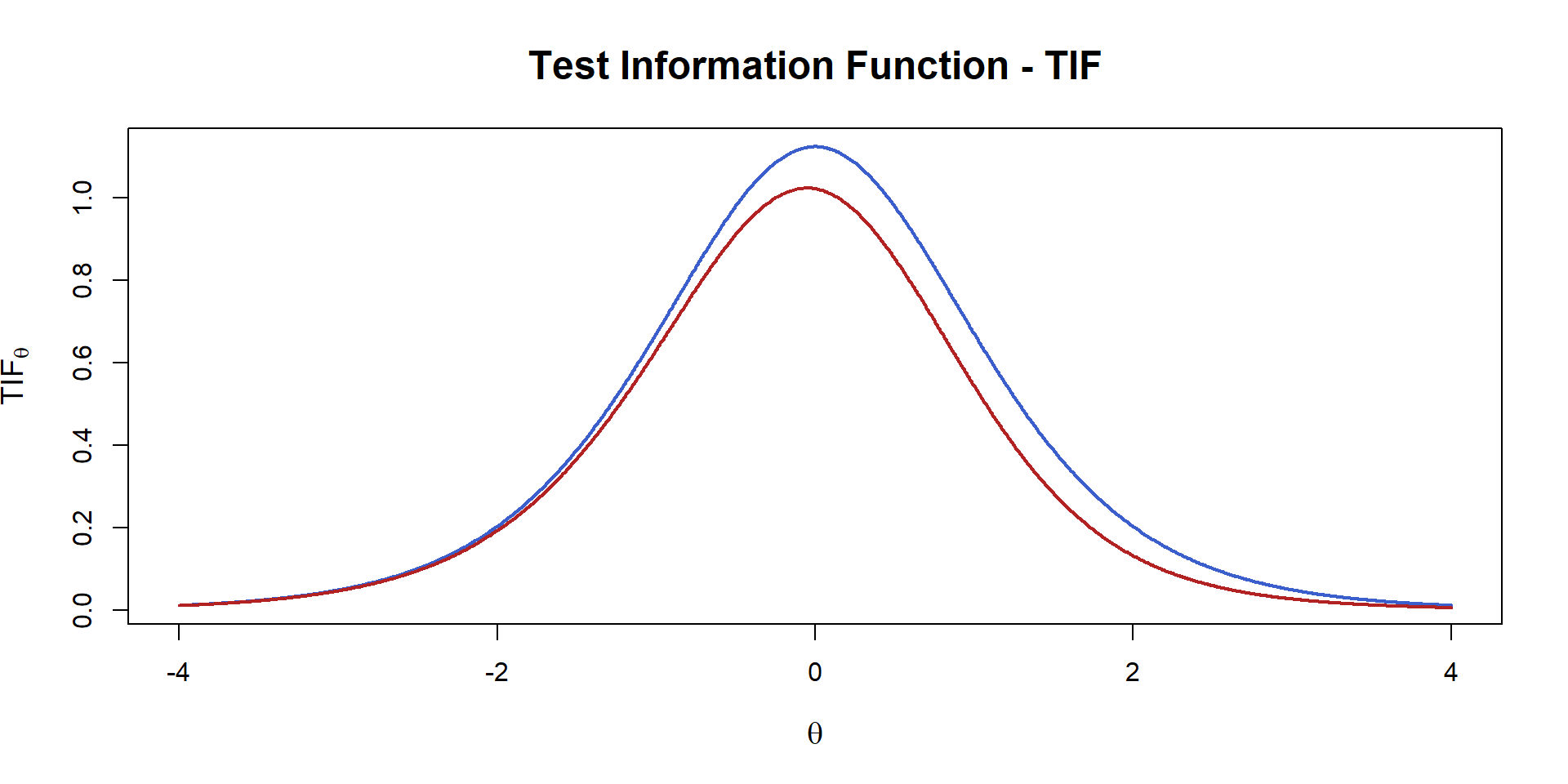
Not a property of the item!
\(d\) depends on the \(r\) rank of the item presentation during the administration, \(d_r\):
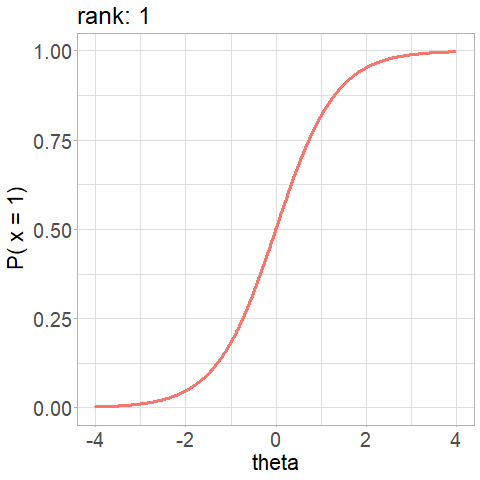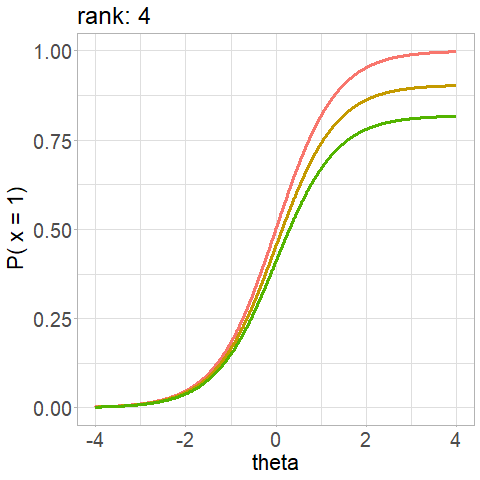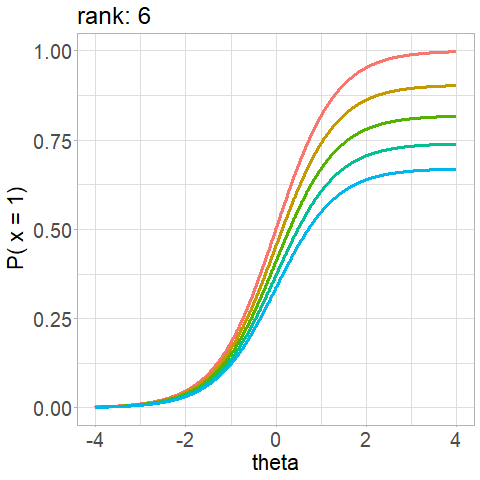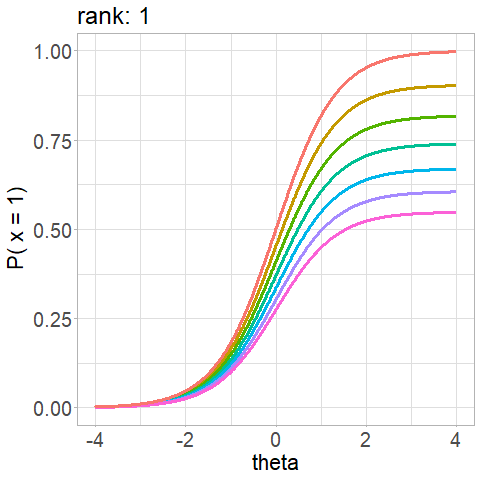
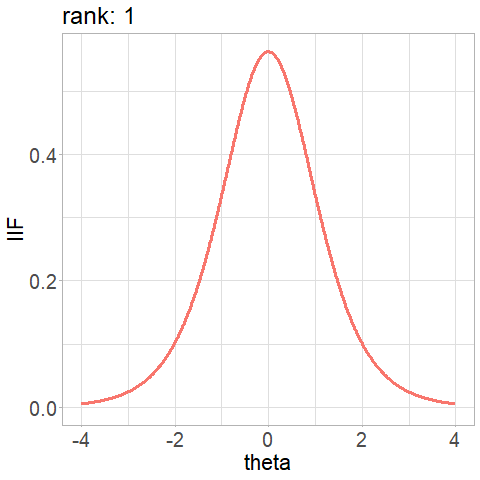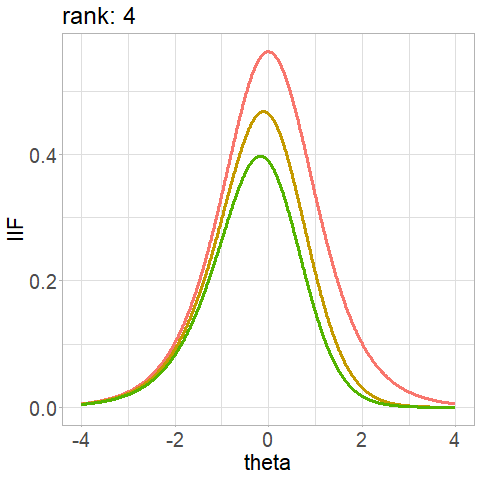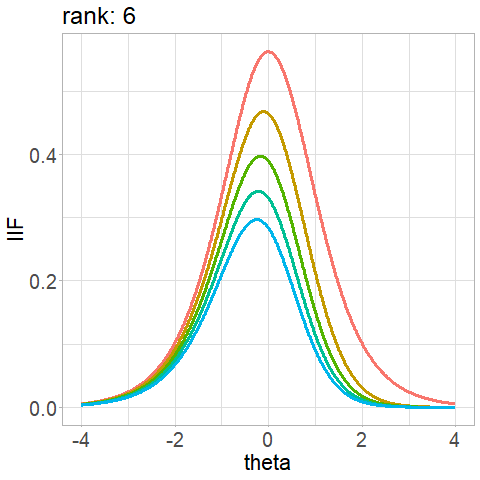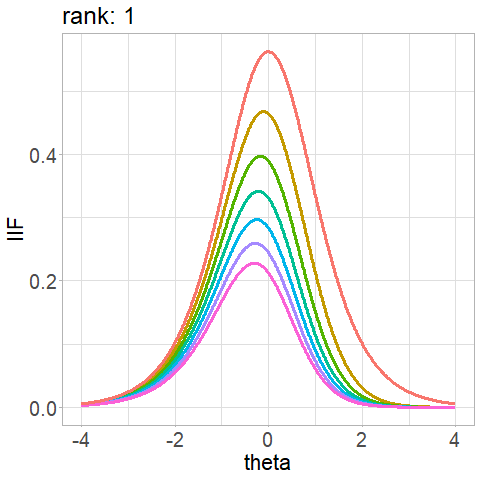
Competing algorithms
\[\text{TIF}^*\]
\[k = 0\]
\[k = 0\]
\[k = 0\]
\[k = 0\]
\[k = 0\]
\[k = 0\]
\[k = 1\]
\[k = 1\]
\[k = 1\]
\[k = 1\]
Frank
At \(k = 0\): \(\text{TIF}^0(\theta) = 0 \, \forall \theta\), \(Q^0 = \emptyset\).
For \(k \geq 0\),
- \(A^k = B \setminus Q^k\)
- \(\forall i \in A^k\), \(p\text{TIF}_{i}^k = \frac{\text{TIF}^k + \text{IIF}_{i}}{||Q^k||+1}\), with \(d_i = 1\), \(\forall i\)
\(i^* = \arg \min_{i \in A^k} (|\text{TIF}^* - \text{pTIF}_i^k|)\)
Termination criterion: \(|\text{TIF}^* - \text{pTIF}_{i^*}^k| \geq |\text{TIF}_B - \text{TIF}^{k}|\):
FALSE: \(Q^{k+1} = Q^{k} \cup \{i^*\}\), \(\text{TIF}^{k+1} = p\text{TIF}_{i^*}\), iterates 1-4
TRUE: Stop, \(Q_{\text{Frank}} = Q^k\)
Léon
At \(k = 0\): \(\text{TIF}^0(\theta) = 0 \, \forall \theta\), \(Q^0 = \emptyset\).
For \(k \geq 0\),
- \(A^k = B \setminus Q^k\)
- \(\forall i \in A^k\), \(p\text{TIF}_{i}^k = \frac{\text{TIF}^k + \text{IIF}_{i}}{||Q^k||+1}\), with \(r = \{0, 1, \ldots, ||Q^k||-1\}\)
\(i^* = \arg \min_{i \in A^k} (|\text{TIF}^* - \text{pTIF}_i^k|)\)
Termination criterion: \(|\text{TIF}^* - \text{pTIF}_{i^*}^k| \geq |\text{TIF}_B - \text{TIF}^{k}|\):
FALSE: \(Q^{k+1} = Q^{k} \cup \{i^*\}\), \(\text{TIF}^{k+1} = p\text{TIF}_{i^*}\), iterates 1-4
TRUE: Stop, \(Q_{\text{Léon}} = Q^k\)
Simulation time
100 replications, item bank \(B'\) of 50 items:
\(b \sim \mathcal{U}(-3, 3)\)
\(a \sim \mathcal{U}(.90, 2.0)\)
\(c_i = 0\), \(\forall i \in B\)
\(d_r = \exp(-0.01 r)\), with \(r = \{0, \ldots, ||B|| -1\}\)
\(\text{TIF}^* = \sum_{i = 1}^{||B'||} \frac{\text{IIF}_i}{||B'||}\), with \(d_i = 1\), \(\forall i \in B'\) 🥇
Considering \(TIF^*\):
Frank: STF from \(B'\) with \(d_i = 1\), \(\forall i \in B'\)
Léon: STF from \(B'\)
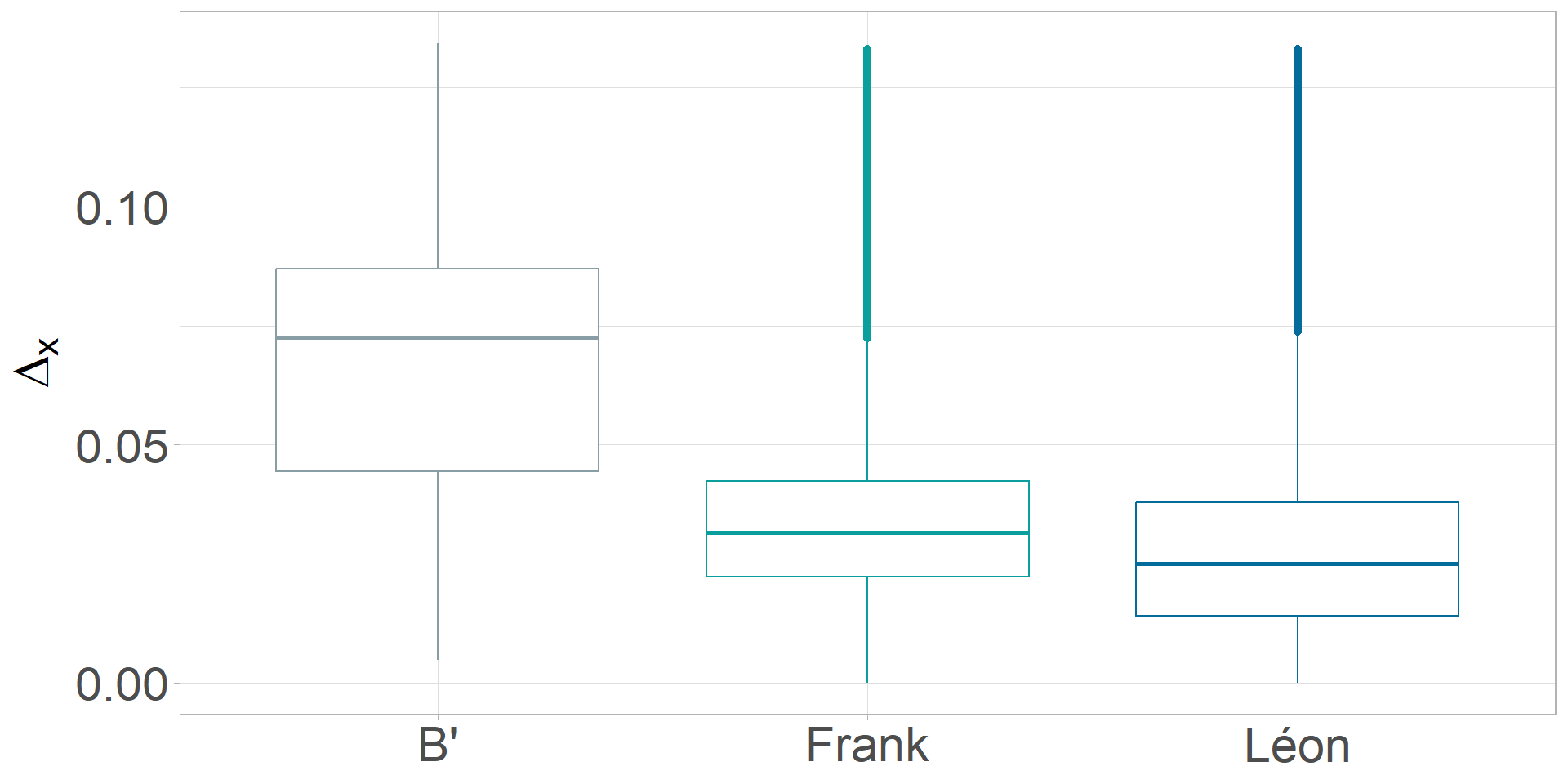
- Distance \(\Delta\) from \(\text{TIF}^*\):
\(\Delta_{\text{all}} = |\text{TIF}^* - \text{TIF}_{B'}|\)
\(\Delta_{\text{Frank}} = |\text{TIF}^* - \text{TIF}_{\text{Frank}}|\)
\(\Delta_{\text{Léon}} = |\text{TIF}^* - \text{TIF}_{\text{Léon}}|\)
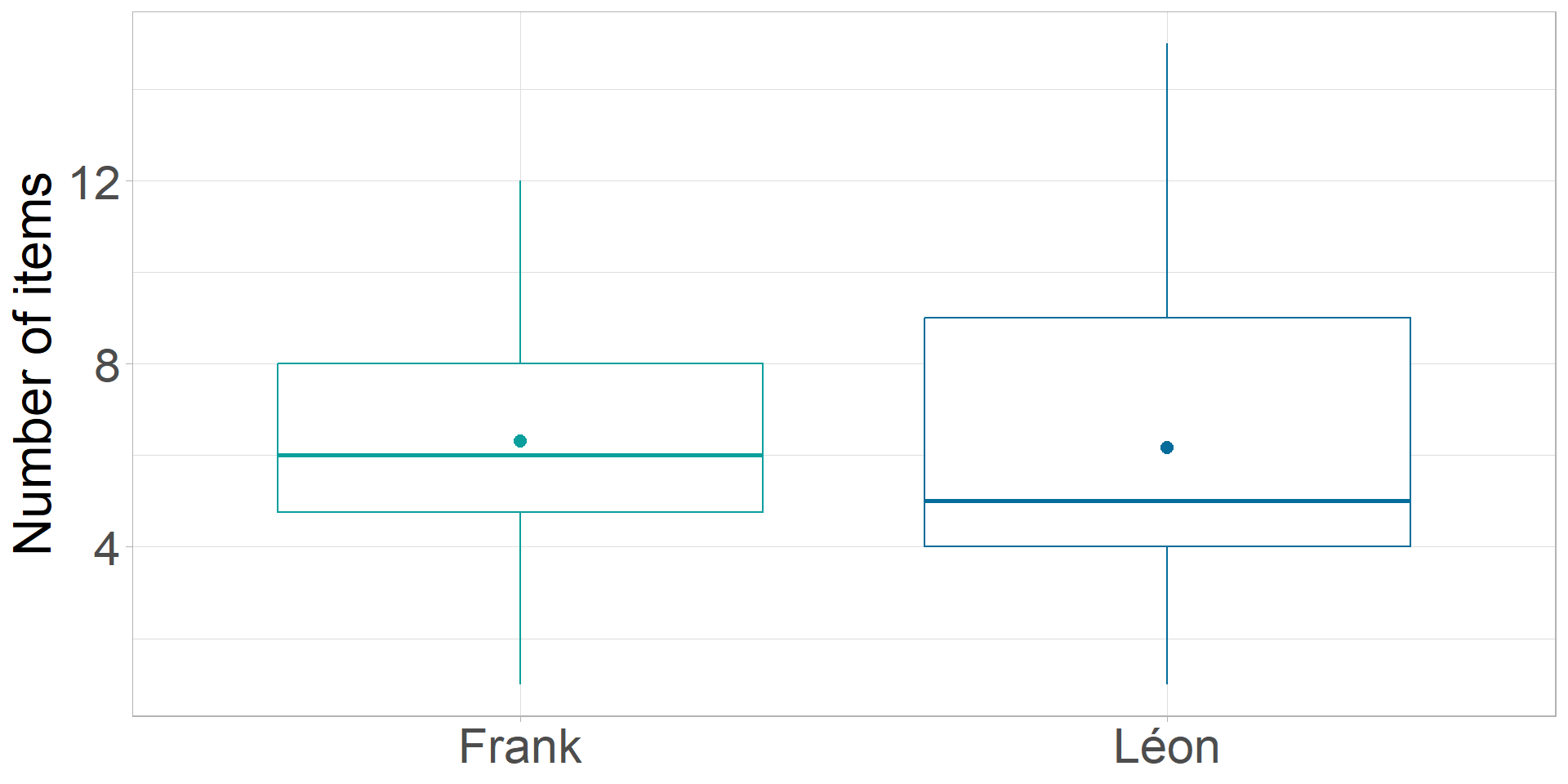
- Number of items selected by Frank and Léon
Results
In the end
The better performance of the short test forms might be due only to the fact that there are less item: What happens if we select random items? We don’t know
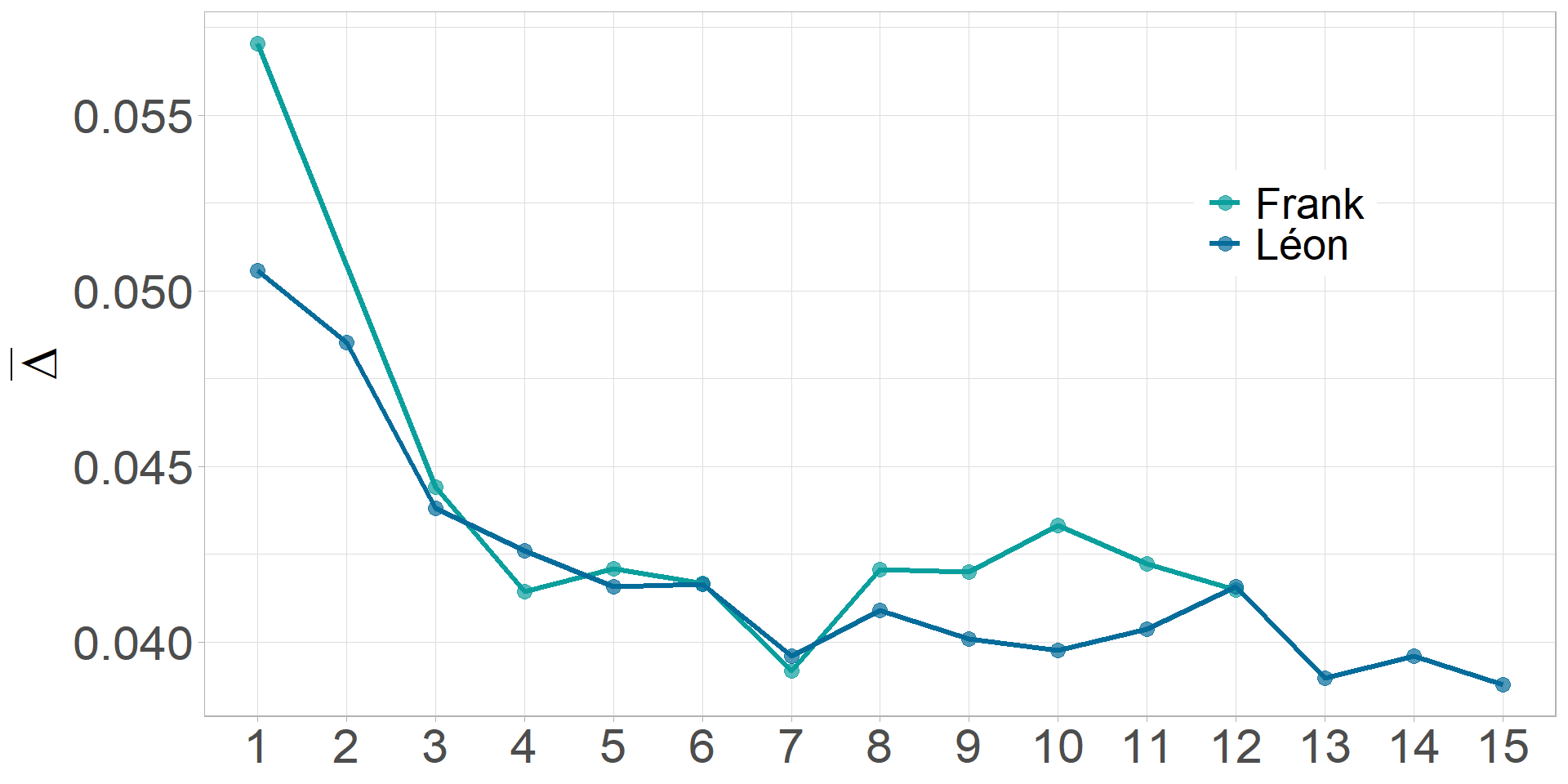
The response fatigue varies as the number of items in the full-length test varies
Approximating the TIF target is not enough: We need to estimate \(\theta\)
SIS 2025, Genova